Chapter 11 Complex Problem - Rotate a List
Question: Rotate a list of numbers so that the number in the first place goes to second, second to third and so on, and finally the last number moves to the first place.
Example
Input - [12, 2, 1, 3, 4, 7, 5, 10, 111, 22]
Output - [22, 12, 1, 3, 2, 4, 7, 5, 10, 111]
11.1 Problem Solving Strategy
The above problem does not appear close to the Python concepts you learned so far. Our challenge here is to translate the real life problems to abstract Python steps like ‘for,’ ‘if’ etc. You can use six steps to accomplish it.
STEP 1. Convert into a small problem: Convert the “general problem” into a specific small problem. So, even if the question asks to write a program for list of any size, assume that the list has only 4 or 5 members.
STEP 2. Solve on paper: Stay away from computer and solve the problem on paper. If I give you four named boxes with four numbers in them, how will you solve the above problem?
Remember the restrictions imposed by Python - 1. a box can have only one number at a time, 2. You can copy one number at a time from one box to another.
STEP 3. Convert the box solution to Python: Do not use any loops at this time.
STEP 4. Use Loops: Think about this situation. Suppose your problem has 10 or 100 numbers instead of 4. What will the code look like? Can the repetitive parts of code be replaced by loop? Rewrite the code using for loop so that the repetitive steps are gone. At this point, do not use range for the loop indices.
STEP 5. Use range: Replace loop index list with a range statement, if you can.
STEP 6. Generalize: Generalize the solution for lists of arbitrary sizes and take care of all corner cases. For generalization, you can write the equivalent code for two different list sizes and see what changes.
11.2 Solving the Rotation Problem
11.2.1 STEP 1. Convert into a small problem
We rewrite the question as -
Rotate a list of four numbers so that the number in the first place goes to second, second to third, third goes to fourth and finally the last number moves to the first place.
Here is an example.
Input - [12, 2, 4, 5]
Output - [5, 12, 2, 4]
11.2.2 STEP 2. Solve on paper
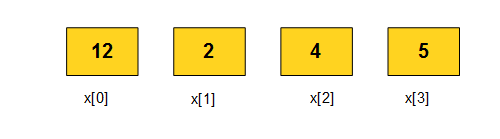
Let us try to solve this problem on paper by drawing boxes with numbers.
Here is the picture of those boxes in the beginning.
Image
Here is the abstract description of what we need to accomplish.
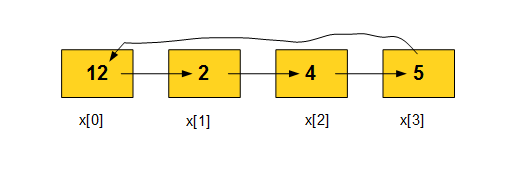
Image
Here is final stage.
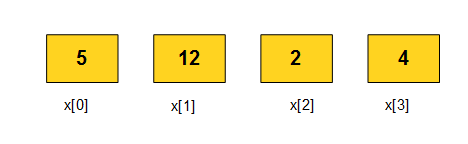
Image
However remember that we have to use Python restrictions. That means at each step, one number from a box gets copied into another box. The number in the original location stays unchanged.
We may attempt to solve through these sequence of operations - 1. copy the number in box x[2] to x[3], 2. copy the number in box x[1] to x[2], 3. copy the number in box x[0] to x[1]
That leaves us with the following numbers in the boxes -
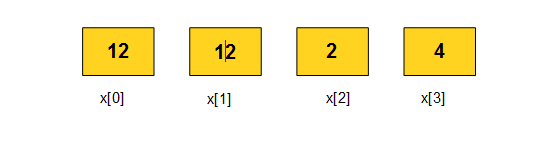
Image
You see that the original number in box x[3] is lost, and we cannot put it in box x[0] any more. To avoid that, we have to add an outside box (let’s call it “tmp”) and copy the number in x[3] as the first step.
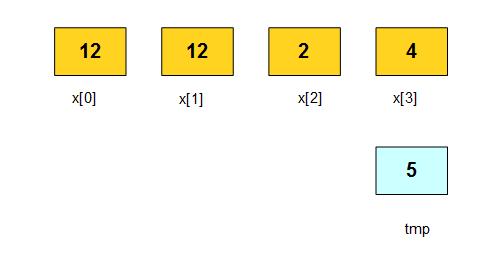
Image
So, the sequence becomes -
- copy the number in box x[3] to tmp,
- copy the number in box x[2] to x[3],
- copy the number in box x[1] to x[2],
- copy the number in box x[0] to x[1],
- copy the number in box tmp to x[0].
11.2.3 STEP 3. Convert the box solution to Python
The above description can be easily converted to Python through the following code.
x=[12, 2, 4, 5]
tmp = x[3]
x[3] = x[2]
x[2] = x[1]
x[1] = x[0]
x[0] = tmp
print(x)As you already know, Python statement “tmp = x[3]” makes Python create a “box” called “tmp” and copy in it the current number in x[3]. If you follow the same logic, you will see that the above code is identical to the solution in step 2.
11.2.4 STEP 4. Convert into Loop
Now think about this situation. Suppose we have a list of 10 numbers instead of 4 numbers. What will the code look like?
x= [12, 2, 1, 3, 4, 7, 5, 10, 111, 22]
tmp=x[9]
x[9]=x[8]
x[8]=x[7]
x[7]=x[6]
x[6]=x[5]
x[5]=x[4]
x[4]=x[3]
x[3]=x[2]
x[2]=x[1]
x[1]=x[0]
x[0]=tmp
print(x)That is a lot of typing, and we should use a loop instead to replace the repetitive part.
x= [12, 2, 1, 3, 4, 7, 5, 10, 111, 22]
tmp =x[9]
for i in [9,8,7,6,5,4,3,2,1]:
x[i]=x[i-1]
x[0]=tmp
print(x)11.2.5 STEP 5. Use Range
We can use range instead of explicit list in the for statement -
x= [12, 2, 1, 3, 4, 7, 5, 10, 111, 22]
tmp=x[9]
for i in range(9,0,-1):
x[i]=x[i-1]
x[0]=tmp
print(x)11.2.6 STEP 6. Generalization
You see that the above code works only for lists of size 10, but we want it to work for all sizes. To generalize, we write the code for different individual sizes and check their differences.
Here is the code for size=10.
x= [12, 2, 1, 3, 4, 7, 5, 10, 111, 22]
tmp=x[9]
for i in range(9,0,-1):
x[i]=x[i-1]
x[0]=tmp
print(x)Similarly, for a list of 4, the solution is -
x=[1,3,4,5]
tmp=x[3]
for i in range(3,0,-1):
x[i]=x[i-1]
x[0]=tmp
print(x)Let us check how the code changed from list-size=10 to list-size=4. you will find that second line changes from tmp=x[9] to tmp=x[3]. Also, the range in the third line changes from 1range(9, 0, -1)range(3,0,-1)`.
What are those numbers 9 and 3? They were one less than the list sizes. We can get the list size from L=len(x).
Therefore the generalized code becomes -
x=[1,2,5,6,7,9]
L=len(x)
tmp=x[L-1]
for i in range(L-1,0,-1):
x[i]=x[i-1]
x[0]=tmp
print(x)11.3 Strategies for Difficult Problems
11.3.1 Develop tests
Tests are not only necessary to check the validity of code, but sometimes they are helpful to understand the question. Therefore, the first step in developing code is to come up with some test scenarios.
11.3.2 Develop an algorithm
The real challenge of programming is not to learn the language, but come up with steps to solve problems. Those steps are called algorithms. Algorithms are usually independent of languages.
11.3.3 Choose a data structure
A data structure like list or dictionary is helpful in holding large collection of data.
11.3.4 Break big problem into small problems
Often a big problem appears to be too complex and new programmers do not where to start. The best solution is to solve a smaller problem that is only part of the original question.
11.3.5 Debug Faulty Code
In one of the earlier supercomputers at University of Illinois, Urbana Champaign, the hardware engineers traced the source of a fauly program to a small bug being stuck between wires. Since then all code errors are called ‘bugs,’ even though cockroaches and spiders moved on to better food than computer parts.
To debug your code -
- Check ‘common mistakes’ in the next section and make sure your code does not have them.
- Use print statement to narrow down the bug.
11.3.6 Make Code Run Faster
If you reach this far, congratulate yourself for writing a working code. Sometime functional code is not enough and you need to improve performance. This can be done by changing the data structures or algorithms.